对数函数 \( y = \log_a x(a>0,a≠1)\) 图象和性质探索

函数图象
对数函数性质总结
| 性质 | a > 1 | 0 < a < 1 |
|---|---|---|
| 定义域 | (0, +∞) | |
| 值域 | R | |
| 定点 | (1, 0) | |
| 当 x > 1 时 | y > 0 | y < 0 |
| 当 0 < x < 1 时 | y < 0 | y > 0 |
| 单调性 | 在(0,+∞)上是增函数 | 在(0,+∞)上是减函数 |
| 当 x 趋近于 0⁺ 时 | y 趋近于 -∞ | y 趋近于 +∞ |
| 当 x 趋近于 +∞ 时 | y 趋近于 +∞ | y 趋近于 -∞ |
| 对称性 | y = log_a x 与 y = log_{1/a} x 关于x轴对称 | |
特殊性质:
- 所有对数函数都经过定点(1,0)
- 对数函数 y = log_a x 和 y = log_{1/a} x 关于x轴对称
- 对数函数是指数函数的反函数,图象关于直线 y=x 对称
- 对数函数在科学计算、金融分析和信息论中有广泛应用
参数控制
0.1
5
注意:a > 0 且 a ≠ 1
常用底数:
函数系列
对数函数知识点
解析式:y = log_2 x
图象:一条上升的曲线,过定点(1,0)
定义域:(0, +∞)
值域:R
单调性:随着x的增大而增大
特殊点:过定点(1,0)
尝试挑战
总积分:
0
/ 10
基础题
积分:
3
求自变量范围
求下列函数的自变量范围:
(1) y = loga x2
(2) \( y = \log_a (4 - x) \)
提高题
积分:
3
比较大小
比较下列各组中两个值的大小:
(1) \( \log_2 3.4, \log_2 8.5 \)
(2) \( \log_{0.3} 1.8, \log_{0.3} 2.7 \)
(3) \( \log_a 5.1, \log_a 5.9 \) (a>0且a≠1)
挑战题
积分:
4
图象分析
如图3所示,有四个对数函数:
① \( y = \log_a x \),② \( y = \log_b x \),
③ \( y = \log_c x \),④ \( y = \log_d x \)
试比较 \( a, b, c, d \) 的大小。
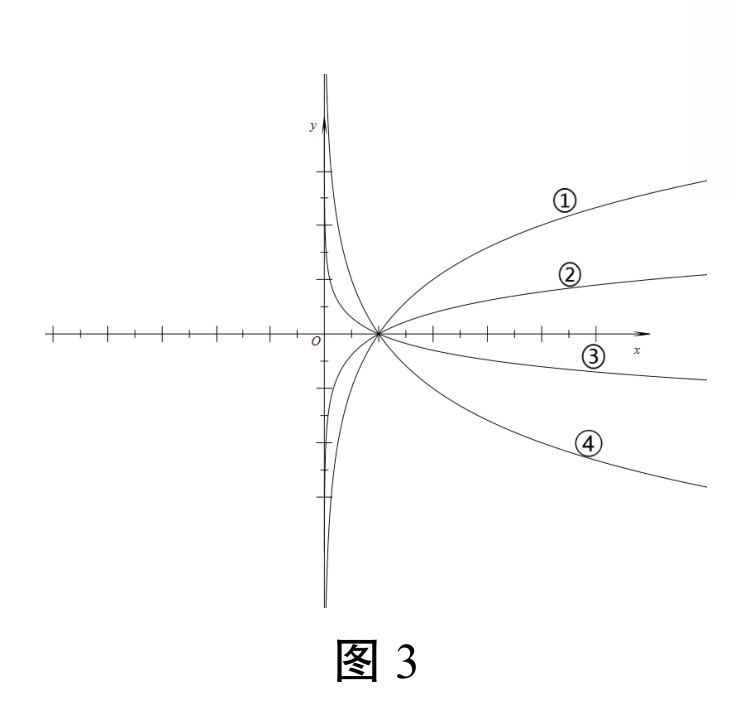
四个对数函数的图象示意图