指数函数y = ax图象和性质探索

函数图象
指数函数性质总结
| 性质 | a > 1 | 0 < a < 1 |
|---|---|---|
| 定义域 | R | |
| 值域 | (0, +∞) | |
| 定点 | (0, 1) | |
| 当 x < 0 时 | 0 < y < 1 | y > 1 |
| 当 x > 0 时 | y > 1 | 0 < y < 1 |
| 单调性 | 在R上是增函数 | 在R上是减函数 |
| 当 x 趋近于正无穷大时 | 函数值y趋近于正无穷大 | 函数值y趋近于0 |
| 当 x 趋近于负无穷大时 | 函数值y趋近于0 | 函数值y趋近于正无穷大 |
特殊性质:
- 所有指数函数都经过定点(0,1)
- 指数函数 y = ax 和 y = (1/a)x 关于y轴对称
- 指数增长/衰减模型在自然科学和社会科学中有广泛应用
参数控制
0.1
5
常用底数:
函数系列
指数函数知识点
解析式:y = 2x
图象:一条上升的曲线,过定点(0,1)
定义域:R
值域:(0, +∞)
单调性:随着x的增大而增大
特殊点:过定点(0,1)
尝试挑战
总积分:
0
/ 10
基础题
积分:
3
比较大小
比较下列两个函数值的大小:
(1) \(1.7^{0.5}, 1.7^{1.5}\)
(2) \(0.8^{-0.2}, 0.8^{1.5}\)
(3) \(1.7^{0.5}, 0.9^{1.9}\)
提高题
积分:
3
图象分析
已知三个指数函数 \(y = a^x\), \(y = b^x\), \(y = c^x\) 的图象如下图所示,比较底数 \(a\), \(b\), \(c\) 的大小:
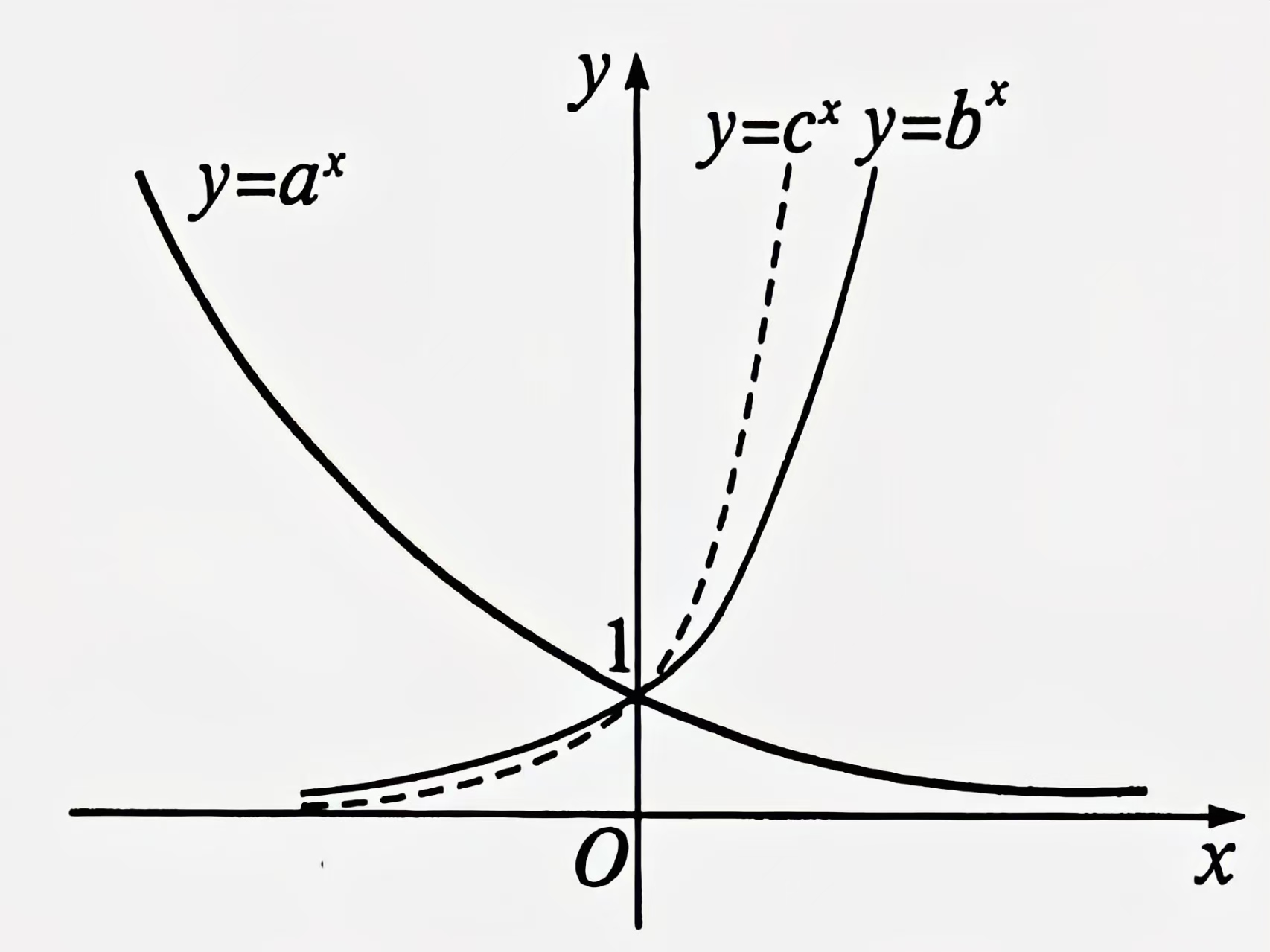
挑战题
积分:
4
函数性质应用
函数 \( y = a^{x-2} + 3 \) (\( a > 0 \) 且 \( a \neq 1 \))的图象恒过定点的坐标为______。
定点坐标:
(
,
)